Greetings! We are Manuel Voelkle from the Max Planck Institute for Human Development in Berlin (Germany) and Han Oud from Radboud University in Nijmegen (The Netherlands). We are both interested in longitudinal data analysis and are trying to advance statistical methods for the analysis of change, as well as to improve their use and communication.
Hot Tip: Longitudinal data analysis is special!
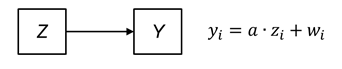
Consider the following model which postulates an effect of Z (e.g., an intervention) on an outcome variable Y:
This model can be interpreted in two different ways: Either in a descriptive way (i.e., it describes the relationship between two variables and can be used to predict Y from Z) or in a causal way (i.e., Z causes Y). Which of the two interpretations is correct is up to the evaluator to find out by means of clever research designs.
What about longitudinal data analysis? In the figure below, we replaced Z by time. This is what we do when we use multilevel models or latent growth curve models as illustrated by the equation to the right.
It is important to realize that this model always remains at the descriptive level. Time never causes anything!
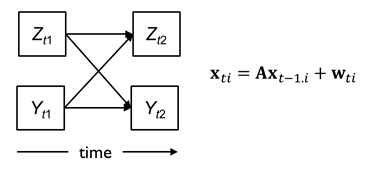
If we are interested in causal mechanisms, we should aim at models like the one shown below, that allow us to study the relationship between variables as they evolve and unfold over time, without time being a predictor.
Hot Tip: Most real-world processes develop continuously over time!
Although extremely useful and popular in modern evaluation research, the latter class of models suffers from the problem that only the order, but not the actual time intervals are taken into account. This causes problems when time intervals are different. For example if a time interval of 1 week is used in one study, but a time interval of 2 weeks in another study, the parameter estimates will be different, but it is unclear whether this is because the actual process, or the time intervals, differed.
Hot Tip: Use continuous time models!
Put more generally, most phenomena in the real world develop continuously over time and should be modeled as such. For this purpose continuous time models have been developed. In short, instead of predicting X directly, we predict the derivative of X with respect to time. This provides us with parameter estimates that are independent of the discrete time intervals a researcher happens to have chosen, and allows us to compare parameter estimates across studies (or individuals) based on different time intervals.
Rad Resources:
This contribution is from the aea365 Tip-a-Day Alerts, by and for evaluators, from the American Evaluation Association. Please consider contributing – send a note of interest to aea365@eval.org. Want to learn more from Manuel and Han? They’ll be presenting as part of the Evaluation 2012 Conference Program, October 24-27 in Minneapolis, MN.

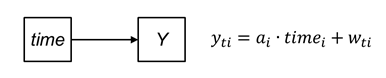
Dear Barbara,
thanks for the question! Continuous time modeling is a statistical tool. It helps you to get more meaningful parameter estimates when analyzing longitudinal data.
For example if you are interested in the relationship between X (e.g., time spent studying) and Y (e.g., test scores) across several school weeks/months/years you may use a continuous time model.
So in order to analyze longitudinal data of annual state content assessment test scores (T=4), you may want to give continuous time models a shot.
You can incorporate an experimental control as well, but this is not a must.
Best,
Manuel
PS. Sorry for the delayed reply! I somehow must have missed your comment…
Hi, Manuel and Han,
Thanks for this most interesting post. Would you be willing to share an example of the latter research design for those of us who are somewhat mathematically challenged? What would a continuous time model look like? Is this an issue of design or can it be done through pure analysis – e.g., if I have longitudinal data made up of 4 years of annual state content assessment test scores, could I do this? Or would I have to have experimental control?